
난이도: Medium
Problem Description
You are in a city that consists of n intersections numbered from 0 to n - 1 with bi-directional roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.
You are given an integer n and a 2D integer array roads where roads[i] = [ui, vi, timei] means that there is a road between intersections ui and vi that takes timei minutes to travel. You want to know in how many ways you can travel from intersection 0 to intersection n - 1 in the shortest amount of time.
Return the number of ways you can arrive at your destination in the shortest amount of time. Since the answer may be large, return it modulo 109 + 7.
Problem Example
Example 1:
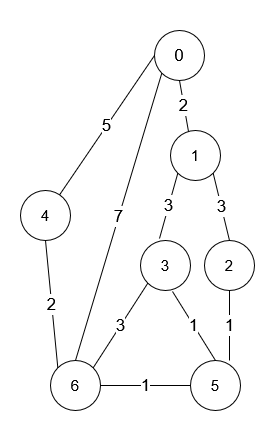
Input: n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
Output: 4
Explanation: The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6Example 2:
Input: n = 2, roads = [[1,0,10]]
Output: 1
Explanation: There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.
Constraints
1 <= n <= 200n - 1 <= roads.length <= n * (n - 1) / 2roads[i].length == 30 <= ui, vi <= n - 11 <= timei <= 109ui != vi- There is at most one road connecting any two intersections.
- You can reach any intersection from any other intersection.
✏️ Solution
class Solution:
def countPaths(self, n: int, roads: List[List[int]]) -> int:
graph = [[] for _ in range(n)]
for v1, v2, cost in roads:
graph[v1].append([v2, cost])
graph[v2].append([v1, cost])
def dijkstra(start, graph, n):
distances = [float('inf')] * n
distances[start] = 0
hq = []
heapq.heappush(hq, (0, start))
path_cnt = [0] * n
path_cnt[0] = 1
while hq:
now_d, now_v = heapq.heappop(hq)
if now_d > distances[now_v]:
continue
for next_v, d in graph[now_v]:
new_d = d + now_d
if new_d < distances[next_v]:
distances[next_v] = new_d
path_cnt[next_v] = path_cnt[now_v]
heapq.heappush(hq, (new_d, next_v))
elif new_d == distances[next_v]:
path_cnt[next_v] = (path_cnt[next_v] + path_cnt[now_v]) % (10 ** 9 + 7)
return path_cnt[-1]
return dijkstra(0, graph, n)다익스트라를 통해 문제를 해결할 수 있었다.
다익스트라를 통해 0번 노드에서 다른 노드까지의 최단 경로를 구하면서 그 경로의 갯수까지 같이 구했다.
다익스트라를 이용해 최단경로의 cost뿐 만 아니라 그 경로의 갯수까지 구할 수 있는 좋은 문제였던 것 같다.
⚙️ Runtime & Memory

문제: 1976. Number of Ways to Arrive at Destination
깃허브: github
algorithmPractice/LeetCode/2090-number-of-ways-to-arrive-at-destination at main · laewonJeong/algorithmPractice
하루 한 문제 챌린지. Contribute to laewonJeong/algorithmPractice development by creating an account on GitHub.
github.com
'알고리즘 > LeetCode' 카테고리의 다른 글
| [LeetCode] 3394. Check if Grid can be Cut into Sections (Python) (0) | 2025.03.25 |
|---|---|
| [LeetCode] 3169. Count Days Without Meetings (Python) (0) | 2025.03.24 |
| [LeetCode] 3108. Minimum Cost Walk in Weighted Graph (Python) (0) | 2025.03.20 |
| [LeetCode] 2401. Longest Nice Subarray (Python) (0) | 2025.03.18 |
| [LeetCode] 2206. Divide Array Into Equal Pairs (Python) (0) | 2025.03.17 |
