
난이도: Medium
Problem Description
You are given an integer n representing the dimensions of an n x n grid, with the origin at the bottom-left corner of the grid. You are also given a 2D array of coordinates rectangles, where rectangles[i] is in the form [startx, starty, endx, endy], representing a rectangle on the grid. Each rectangle is defined as follows:
(startx, starty): The bottom-left corner of the rectangle.(endx, endy): The top-right corner of the rectangle.
Note that the rectangles do not overlap. Your task is to determine if it is possible to make either two horizontal or two vertical cuts on the grid such that:
- Each of the three resulting sections formed by the cuts contains at least one rectangle.
- Every rectangle belongs to exactly one section.
Return true if such cuts can be made; otherwise, return false.
Problem Example
Example 1:
Input: n = 5, rectangles = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]]
Output: true
Explanation:
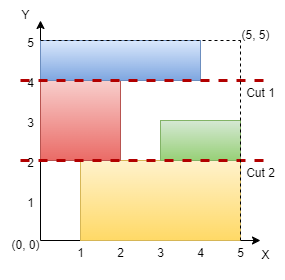
The grid is shown in the diagram. We can make horizontal cuts at y = 2 and y = 4. Hence, output is true.
Example 2:
Input: n = 4, rectangles = [[0,0,1,1],[2,0,3,4],[0,2,2,3],[3,0,4,3]]
Output: true
Explanation:
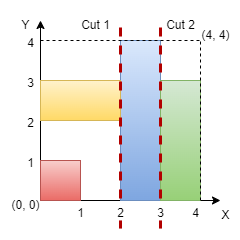
We can make vertical cuts at x = 2 and x = 3. Hence, output is true.
Example 3:
Input: n = 4, rectangles = [[0,2,2,4],[1,0,3,2],[2,2,3,4],[3,0,4,2],[3,2,4,4]]
Output: false
Explanation:
We cannot make two horizontal or two vertical cuts that satisfy the conditions. Hence, output is false.
Constraints
3 <= n <= 1093 <= rectangles.length <= 1050 <= rectangles[i][0] < rectangles[i][2] <= n0 <= rectangles[i][1] < rectangles[i][3] <= n- No two rectangles overlap.
✏️ Solution
class Solution:
def checkValidCuts(self, n: int, rectangles: List[List[int]]) -> bool:
n = len(rectangles)
def can_cut(rectangles, dir):
rectangles.sort(key = lambda x:x[dir])
result = 0
max_end = rectangles[0][dir+2]
for i in range(1, n):
start = rectangles[i][dir]
end = rectangles[i][dir+2]
if max_end <= start:
result += 1
if result == 2:
return True
max_end = max(max_end, end)
return result > 1
return can_cut(rectangles, 0) or can_cut(rectangles, 1)어제 문제와 같은 유형의 문제였던 것 같다.
결국 가로 줄이나 세로 줄을 3개로 나누었을 때, 그 구간에 겹치는 사각형이 없이 완전한 사각형이 있으면 된다.
나는 can_cut 함수를 구현하여 이를 판단했다.
먼저 사각형들을 dir 방향 기준으로 정렬한 후, 겹치지 않는 구간을 찾았다.
max_end 변수를 사용하여 현재까지의 최대 끝 지점을 관리하면서, 연속된 사각형들이 겹치지 않으면 result를 증가시켰다.
만약 겹친다면 같은 구간에 있어야 한다고 판단해 result를 건드리지 않는다.
이 때 result > 1을 통해 3개로 나누었을 때, 모든 사각형이 자른 구간에 완전히 들어갈 수 있는지 결과를 return하였다.
마지막에는 can_cut함수를 통해 정답을 맞출 수 있었다.
⚙️ Runtime & Memory

문제: 3394. Check if Grid can be Cut into Sections
깃허브: github
algorithmPractice/LeetCode/3657-check-if-grid-can-be-cut-into-sections at main · laewonJeong/algorithmPractice
하루 한 문제 챌린지. Contribute to laewonJeong/algorithmPractice development by creating an account on GitHub.
github.com
'알고리즘 > LeetCode' 카테고리의 다른 글
| [LeetCode] 2780. Minimum Index of a Valid Split (Python) (0) | 2025.03.27 |
|---|---|
| [LeetCode] 2033. Minimum Operations to Make a Uni-Value Grid (Python) (0) | 2025.03.26 |
| [LeetCode] 3169. Count Days Without Meetings (Python) (0) | 2025.03.24 |
| [LeetCode] 1976. Number of Ways to Arrive at Destination (Python) (0) | 2025.03.23 |
| [LeetCode] 3108. Minimum Cost Walk in Weighted Graph (Python) (0) | 2025.03.20 |
