[LeetCode] 1028. Recover a Tree From Preorder Traversal (Python)

 

 

난이도: Hard

문제 설명

---

We run a preorder depth-first search (DFS) on the root of a binary tree.

 

At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node.  If the depth of a node is D, the depth of its immediate child is D + 1.  The depth of the root node is 0.

 

If a node has only one child, that child is guaranteed to be the left child.

 

Given the output traversal of this traversal, recover the tree and return its root.

 

문제 예제

---

Example 1:

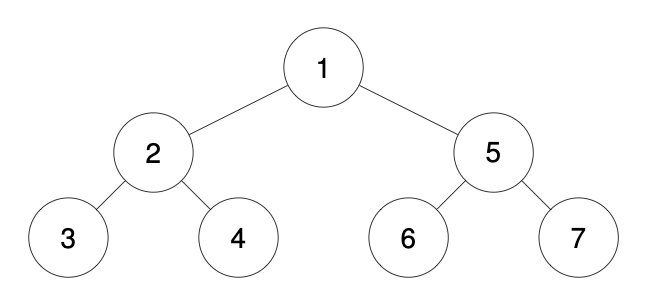
Input: traversal = "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]

Example 2:

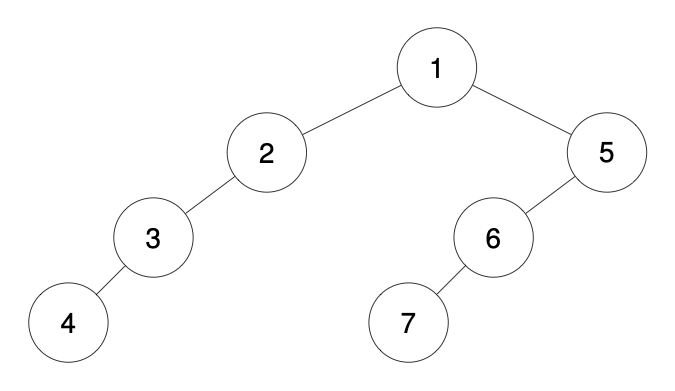
Input: traversal = "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]

Example 3:

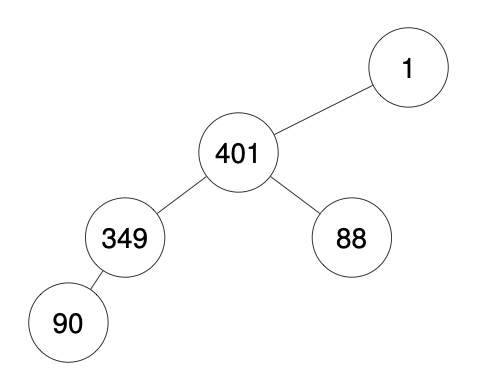
Input: traversal = "1-401--349---90--88"
Output: [1,401,null,349,88,90]

 

제한 사항

---

• The number of nodes in the original tree is in the range [1, 1000].
• 1 <= Node.val <= 109

 

✏️ Solution(솔루션)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def recoverFromPreorder(self, traversal: str) -> Optional[TreeNode]:
        nodes = []
        n = len(traversal)

        i = 0
        dash = 0
        digit = 0
        while i != n:
            if traversal[i].isdigit():
                if dash:
                    nodes.append(dash)
                    dash = 0
                digit= digit*10 + int(traversal[i])
            else:
                if digit:
                    nodes.append(digit)
                    digit=0
                dash += 1
            i+=1

        nodes.append(digit) # nodes = [1, '-', 401, '--', 349, '---', 90, '--', 88]
        n = len(nodes)
        root = TreeNode(nodes[0])
        
        def dfs(root, idx, depth):
            for lr in range(2):
                if idx + 2 < n and depth+1 == nodes[idx+1]:
                    if lr == 0:
                        root.left = TreeNode(nodes[idx+2])
                        idx = dfs(root.left, idx+2, depth+1)
                    else:
                        root.right = TreeNode(nodes[idx+2])
                        idx = dfs(root.right, idx+2, depth+1)
                else:
                    return idx
            return idx
        
        dfs(root, 0, 0)
        return root

 

 

어려운 문제 였다..

 

처음에는 대쉬를 기준으로 graph를 만들고, graph와 연결된 자식들을 root.left = graph[i][0], root.right = graph[i][1]으로 트리를 만들어 반환했는데 Memory Limit Exceed가 발생했다..

( ex) input: traversal = 1-2--3--4-5--6--7  ==> graph = {1: [2,5], 2:[3,4], 5:[6,7]})

 

아마 graph를 만들어서 그런거지 않을까 하고 graph를 만들지 않고 트리를 만들려고 해봤다.

 

그러다가 dfs를 통해 가능하지 않을까 싶어서 이를 구현했다.

 

현재 depth + 1과 다음 depth와 같다면 root의 왼쪽 자식을 추가 해주었다. 만약 다르다고 한다면 다시 쭉 돌아가서 root의 오른쪽 자식을 추가해주었다.

 

dfs연산이 끝나면 트리를 반환하고 정답을 맞출 수 있었다.

 

dfs 코드 짜는데도 시간이 굉장히 오래걸린 것 같다..

 

다시 한번 풀어보면 좋을 것 같다...

 

⚙️ Runtime & Memory

---

 

 

---

문제: 1028. Recover a Tree From Preorder Traversal 

 

깃허브: github

algorithmPractice/LeetCode/1093-recover-a-tree-from-preorder-traversal at main · laewonJeong/algorithmPractice